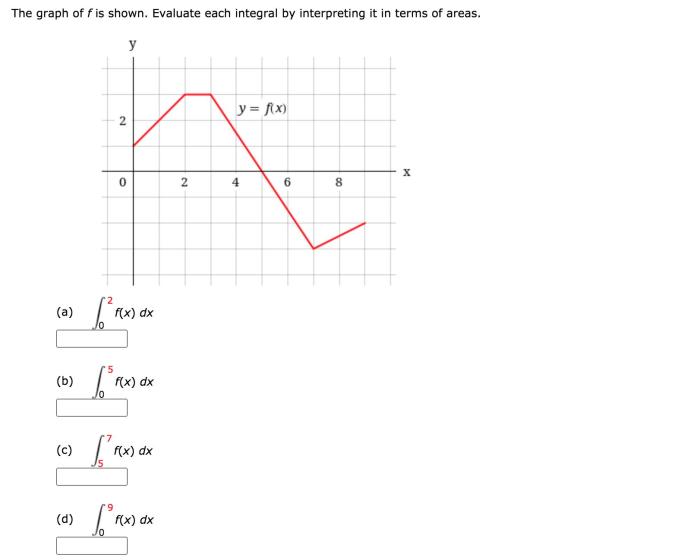
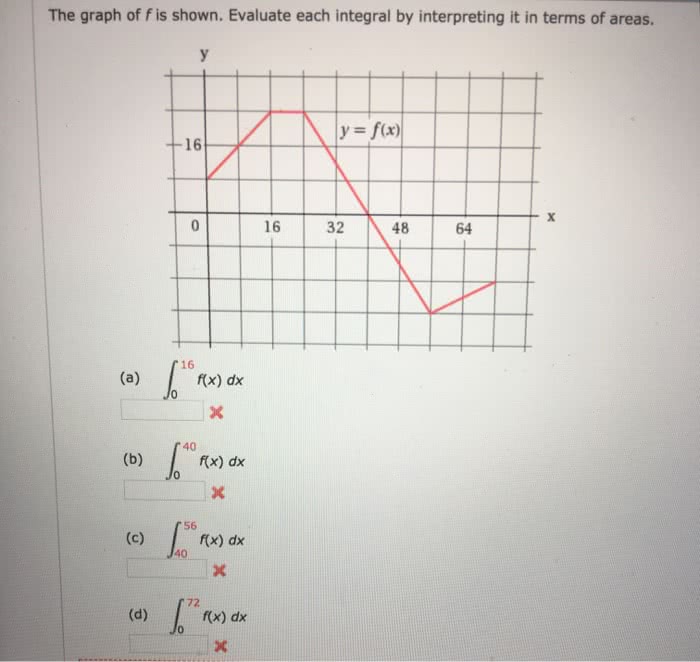
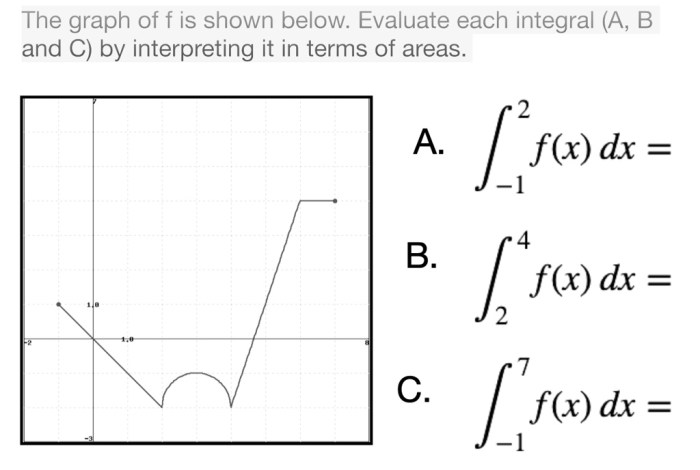
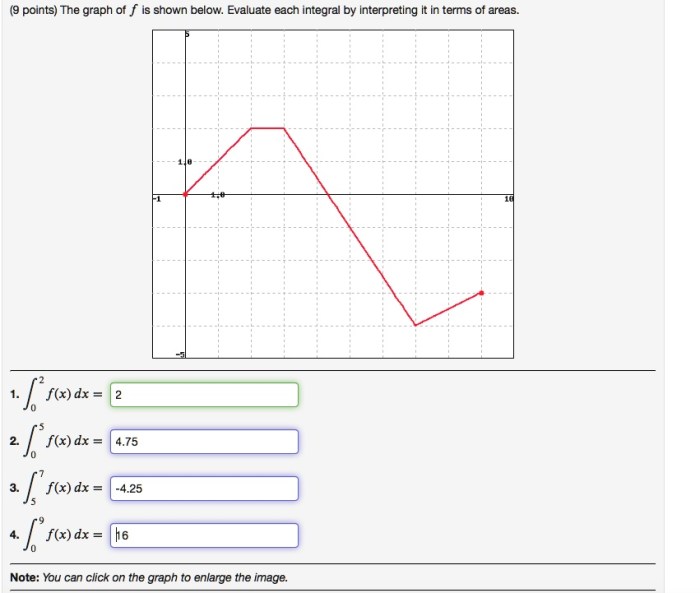
Evaluate each integral by interpreting it in terms of areas. – Evaluate each integral by interpreting it in terms of areas, a fundamental concept in calculus, provides a powerful tool for understanding and solving a wide range of mathematical problems. By interpreting integrals as areas under curves, we gain valuable insights into their geometric significance and practical applications.
This comprehensive guide explores the concept of integral evaluation through the lens of area interpretation, examining various geometric shapes, definite and indefinite integrals, and their applications in diverse fields.
Integral as Area under a Curve
An integral can be interpreted as the area under the curve of a function. This interpretation is fundamental in understanding the concept of integration and its applications in various fields.
For example, consider the integral ∫[0,2] x^2 dx. This integral represents the area under the curve of the function f(x) = x^2, between the limits x = 0 and x = 2. The area can be visualized as a triangle with base 2 and height 4, resulting in an area of 4 square units.
Evaluating Integrals using Geometric Shapes
Integrals can be evaluated by dividing the area under the curve into geometric shapes, such as rectangles, triangles, and trapezoids. By approximating the area of each shape and summing them up, we can estimate the total area under the curve.
- Rectangles:Divide the area into rectangles with equal width and approximate the area of each rectangle as the product of width and height.
- Triangles:Divide the area into triangles with equal base and height, and approximate the area of each triangle as half the product of base and height.
- Trapezoids:Divide the area into trapezoids with equal height and parallel bases, and approximate the area of each trapezoid as the average of the bases multiplied by the height.
Definite and Indefinite Integrals
Integrals can be classified into definite and indefinite integrals based on the presence of limits of integration.
- Definite Integrals:Integrals with specified lower and upper limits represent the area under the curve between those limits. They are denoted as ∫[a,b] f(x) dx.
- Indefinite Integrals:Integrals without specified limits represent the area under the curve for all values of x. They are denoted as ∫ f(x) dx.
Applications of Integral Evaluation
Integral evaluation has numerous practical applications in various fields, including:
- Physics:Calculating work done, force, and potential energy.
- Engineering:Determining volumes, centroids, and moments of inertia.
- Economics:Calculating consumer surplus, producer surplus, and elasticities.
Numerical Integration Methods, Evaluate each integral by interpreting it in terms of areas.
Numerical integration methods provide approximate solutions to integrals when analytical solutions are difficult or impossible to obtain. These methods include:
- Trapezoidal Rule:Approximates the area under the curve using a series of trapezoids.
- Simpson’s Rule:A more accurate method that uses a series of parabolas to approximate the area.
FAQs: Evaluate Each Integral By Interpreting It In Terms Of Areas.
What is the geometric interpretation of an integral?
An integral can be interpreted as the area under the curve of a function over a given interval.
How can we use geometric shapes to evaluate integrals?
We can approximate the area under a curve by dividing it into rectangles, triangles, or trapezoids and calculating their areas.
What is the difference between definite and indefinite integrals in terms of area interpretation?
A definite integral represents the exact area under a curve over a specified interval, while an indefinite integral represents the family of all antiderivatives of the function.