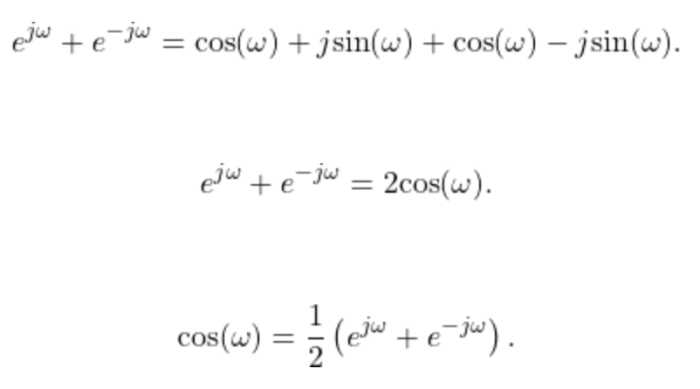Use euler’s formula to find the missing number – Unveiling the enigmatic world of complex numbers, this comprehensive guide delves into the intricacies of Euler’s formula and its remarkable applications in solving missing number problems. As we embark on this mathematical journey, we will explore the formula’s elegance and versatility, unraveling its power to unlock hidden values in a myriad of real-world scenarios.
Euler’s formula, e^(ix) = cos(x) + i sin(x), establishes a profound connection between the exponential function and trigonometry, enabling us to represent complex numbers in a polar form. This formula serves as a cornerstone for understanding the behavior of complex numbers and their applications in various scientific and engineering disciplines.
Understanding Euler’s Formula: Use Euler’s Formula To Find The Missing Number
Euler’s formula is a mathematical identity that relates the exponential function to the trigonometric functions. It states that for any real number x, e^(ix) = cos(x) + i sin(x), where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the cosine and sine functions, respectively.
This formula provides a deep connection between complex numbers and trigonometry. It allows us to represent complex numbers in terms of their real and imaginary parts, and to perform trigonometric operations on them.
Finding Missing Numbers Using Euler’s Formula
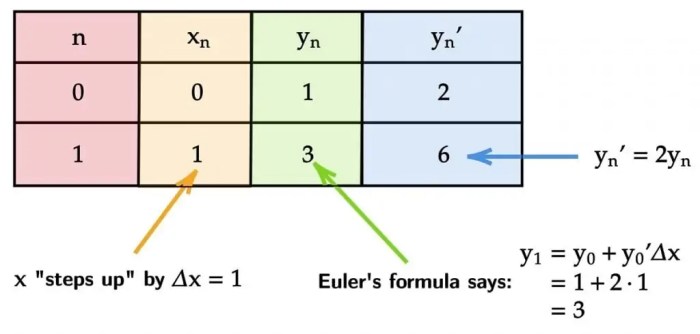
Euler’s formula can be used to find missing numbers in a sequence of complex numbers. For example, if we have a sequence of complex numbers z1, z2, …, zn, and we know the values of z1, z2, …, zk-1, zk+1, …, zn, we can use Euler’s formula to find the value of zk.
To do this, we first convert the complex numbers to their exponential form. Then, we use the fact that e^(ix) = cos(x) + i sin(x) to write the complex numbers in terms of their real and imaginary parts. Finally, we use the known values of the real and imaginary parts to solve for the unknown value of zk.
Applications of Euler’s Formula in Missing Number Problems
Euler’s formula has a wide range of applications in missing number problems. For example, it can be used to:
- Find the missing term in a geometric sequence of complex numbers.
- Find the roots of a polynomial equation with complex coefficients.
- Solve systems of linear equations with complex coefficients.
Limitations and Considerations, Use euler’s formula to find the missing number
While Euler’s formula is a powerful tool for finding missing numbers, it does have some limitations. For example, it may not be applicable if the complex numbers in the sequence are not all distinct. Additionally, the formula may lead to multiple solutions, which can make it difficult to determine the correct value of the missing number.
Advanced Techniques for Missing Number Problems
In some cases, more advanced mathematical techniques may be needed to find missing numbers in a sequence of complex numbers. These techniques include:
- Complex analysis
- Numerical methods
- Other approaches, such as using the theory of residues
Essential Questionnaire
What is Euler’s formula?
Euler’s formula is a mathematical identity that establishes a profound connection between the exponential function and trigonometry, given by e^(ix) = cos(x) + i sin(x), where e is the base of the natural logarithm, i is the imaginary unit, and x is a real number.
How is Euler’s formula used to find missing numbers?
Euler’s formula can be used to find missing numbers in a sequence by expressing the terms of the sequence in terms of complex numbers and then using the formula to solve for the unknown values.
What are the limitations of using Euler’s formula to find missing numbers?
Euler’s formula may not be applicable in all cases, such as when the missing number is not a complex number or when the formula leads to multiple possible solutions.
What are some advanced techniques that complement Euler’s formula for missing number problems?
Advanced techniques that complement Euler’s formula include complex analysis, numerical methods, and other mathematical approaches that can handle more complex missing number problems.